「線形補間」という言葉を見ると、
数式が出てきそうで少し身構えてしまいます。
でも、やっていることはとてもシンプルです。
線の上を、どれくらい進んだかを表しているだけです。
線形補間は
「2 つの場所の間を、どれくらい進んだか」
まずは図で考える
左 右
•-------------------->
●
↑
どれくらい進んだか
これは
- 左から
- 右に向かって
- どれくらい進んだか
を求めているだけです。
どれくらい進んだか。
その結果の「位置」を求めています。
式はあとからついてきた説明にすぎません。
練習問題①
まずは、とてもシンプルな問題です。
問題
左が 0、右が 10 です。
その間を、ちょうど真ん中まで進んだとします。
そのときの数はいくつでしょうか?
(少し考えてみてください)
ヒント
- 0 から 10 まであります
- 真ん中とは、半分のところです
答え
5 です。
なぜ 5 なのか
0 から 10 までの長さは 10。
その半分は 5。
つまり、
左から右に向かって、
ちょうど半分だけ進んだ位置 が 5 です。
0 10
•-------------------->
↑
5
練習問題②
問題
左が 10、右が 20 です。
その間を、4 分の 1 だけ進んだとします。
そのときの数はいくつでしょうか?
(少し考えてみてください)
ヒント
- 10 から 20 までは、全部でいくつありますか?
- 4 分の 1 とは、そのうちのどれくらいですか?
答え
12.5 です。
なぜ 12.5 なのか
10 から 20 までの長さは 10。
その 4 分の 1 は 2.5。
つまり、
左から右に向かって、
2.5 だけ進んだ位置が答えです。
10 + 2.5 = 12.5
図で見ると
10 -------------------- 20
↑
12.5
「真ん中」ではなくても、
- まず全体の長さを見る
- どれくらい進むかを決める
- それを足す
という考え方は同じです。
練習問題③
問題
左が 20、右が 10 です。
その間を、3 割だけ進んだとします。
そのときの数はいくつでしょうか?
(少し考えてみてください)
ヒント
- 20 から 10 までは、どれくらいの長さがありますか?
- 3 割とは、そのうちのどれくらいですか?
- 今回は「小さくなる方向」に進みます
答え
17 です。
なぜ 17 なのか
20 から 10 までの長さは 10。
3 割は、そのうちの 3。
つまり、
20 から 3 だけ進むと 17 になります。
今回は
- 足すのではなく
- 引く
という違いがありますが、
やっていることは同じです。
図で見ると
20 -------------------- 10
↑
17
右に向かって進んでいるので、
数は小さくなります。
ここで大事なこと
向きが変わっても、
- 全体の長さを見る
- どれくらい進むかを決める
- その分だけ動かす
という考え方は変わりません。
線形補間は、
増えるか減るかではなく、
どれくらい進むかを決めているだけ です。
練習問題④
問題
左が 100、右が 108 です。
その間を、0.75 だけ進んだとします。
そのときの数はいくつでしょうか?
(少し考えてみてください)
ヒント
- 100 から 108 までは、全部でいくつありますか?
- 0.75 とは、「1 のうち 0.75」です
- つまり「全部のうち 75%」ということです
答え
106 です。
なぜ 106 なのか
100 から 108 までの長さは 8。
その 0.75 は、
8 × 0.75 = 6
つまり、
100 から 6 進んだ位置なので、
106 になります。
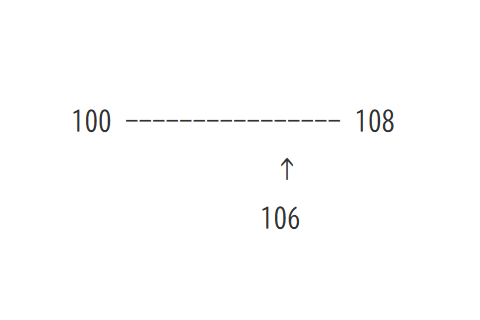
図で見ると
100 ---------------- 108
↑
106
ここで大事なこと
小数になっても、
- 全体の長さを見る
- どれくらい進むかを決める
- その分だけ動かす
という考え方は変わりません。
「0.75」は特別な数字ではなく、
“どれくらい進むか”を表しているだけ です。
練習問題⑤
問題
左が 0、右が 10 です。
その間を、1.2 だけ進んだとします。
そのときの数はいくつでしょうか?
(少し考えてみてください)
ヒント
- 0 から 10 までは、全部で 10
- 「1」は、ちょうど右端まで進んだ状態
- 「1.2」は、それよりも少し多く進んだ状態
答え
12 です。
なぜ 12 なのか
0 から 10 までの長さは 10。
1.0 進むと 10 に着きます。
1.2 ということは、
10 を全部進んで、
さらに 0.2 進むということです。
10 の 0.2 は 2。
つまり、
10 を通りすぎて 2 だけ進んだ位置。
答えは 12 になります。
図で見ると
0 ---------- 10 -----
↑
12
ここで大事なこと
「1」をこえても、
やっていることは同じです。
- 全体の長さを見る
- どれくらい進むかを決める
- その分だけ動かす
ただ、少し“はみ出した”だけです。
5 問を通して
ここまでの問題でわかることは、
線形補間は、
- 真ん中を求めるものでもなく
- 割合を計算するものでもなく
- 増やす・減らすテクニックでもなく
ただ、
2つの場所の間を、どれくらい進んだか
を表しているだけ、ということです。
最後に式で表すと
ここまでやってきたことを、
式で表現してみると、こうなります。
答え = 左 +(右 − 左)× どれくらい進んだか
さきほど図で考えた練習問題④を、今度はこの式で解いてみます。
この式で練習問題④を解いてみましょう
問題
左が 100、右が 108 です。
その間を、0.75 だけ進んだとします。
そのときの数はいくつでしょうか?
計算
左 = 100
右 = 108
どれくらい進んだか = 0.75
式に当てはめると:
答え
= 100 + (108 − 100) × 0.75
= 100 + 8 × 0.75
= 100 + 6
= 106
ちゃんと、さきほどの答えと同じになりました。
式は、新しい考え方ではなく、
これまでやってきたことを短く書いただけです。